Estructura Atómica
Enlace Químico
Termodinámica química
Equilibrio Químico
Ácido Base
Redox
SelectividadContenido del Vídeo
En este último ejercicio resuelto del tema de Cinética Química, calcularemos distintos valores de una reacción química utilizando la ecuación de Arrhenius linealizada, es decir:
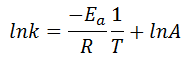
En concreto, debemos calcular la energía de activación (partiendo de la constante de velocidad a dos temperaturas distintas), el factor preexponencial o factor de frecuencia, A, y la constante de velocidad a una tercera temperatura. El enunciado completo es:
Para la reacción A+B → C, se tienen los siguientes datos:
|
T |
k (mol-1·L·s-1) |
|
600 |
0,385 |
| 716 |
16,0 |
Calcular la energía de activación, Ea, el factor de frecuencia, A, y la constante de velocidad a 800K.
También te puede interesar:
Cinética Química Teoría 8: Ecuación de Arrhenius
Cinética Química Ejercicio 16: Calcular la constante de velocidad con la ecuación de Arrhenius
Category: Cinética Química y Ejercicios de Cinética Química.
Etiquetas: Ecuación de Arrhenius y Energía de activación.
cuando uso la formula logaritmica y cuando la otra??
irene, 9 Años Antes
¡Hola! Si dispones únicamente del valor a una temperatura dada y te dan el valor de A (factor preexponencial) puedes usar la exponencial. En cambio, si por ejemplo no tienes el valor de A y tienes el valor de energía de activación a dos temperaturas distintas, o el valor de la constante de velocidad, tendrás que usar la logarítmica. Esta última es más útil y utilizada que la exponencial. Espero haberte aclarado. Un saludo grande.
QuimiTube, 9 Años Antes
Podrías ayudarme con el calculo de A? Cuando despejo me queda que lnA=8.28^6 lo cual da infinito.
me gustaría saber como hiciste ese calculo porque pasas directamente al resultado de A y no puedo hacerlo.
Desde ya muy agradecido.
Gabriel, 9 Años Antes